Chances are you've seen a neural network diagram like this one with circles and arrows:
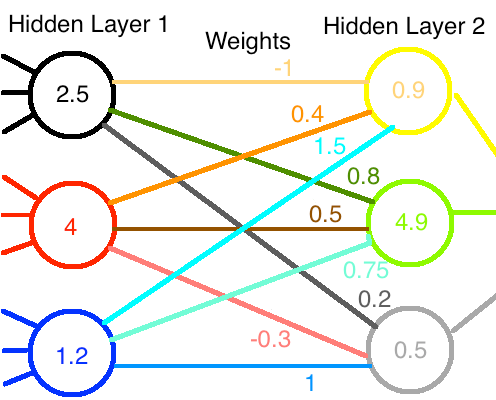Figure: A neural network. Source: Medium
While that looks fancy, it's basically a matrix. More generally, it's a tensor, but a special kind of tensor which makes it just a matrix.
I was reading this Medium article comparing matrices and tensors which models the following matrix multiplication as the two-layer neural network shown above:
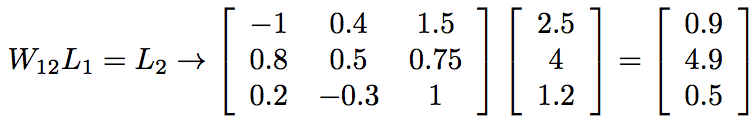
This helped me realize that any linear map can be modeled as a neutral network. Consider rotating a vector around the X, then Y, and Z-axes:
$$ \begin{aligned} M_x &= Rot_x(15°) \newline M_y &= Rot_y(15°) \newline M_z &= Rot_z(15°) \newline V &= [1,2,3] \newline V' &= M_xV \newline &= [1, \pmb{1.155}, \pmb{3.415}] \newline V'' &= M_yV' \newline &= [\pmb{1.850}, 1.155, \pmb{3.042}] \newline V''' &= M_zV'' \newline &= [\pmb{1.488}, \pmb{1.595}, 3.042] \newline \end{aligned} $$
Here is a neural network visualizing the linear mapping sequence $M_zM_yM_xV$:
Figure: Made with draw.io
By tracing the paths through the layers of the neural network below, one can gain an intuition of how each transformation operation contributes to the resulting vector $V_{rot}$.
Figure: Made with draw.io